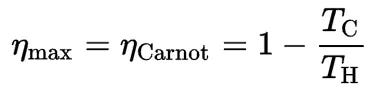Firehose #185: ☀️ Climate invariants. ☀️

How physical constraints inspire business model innovation, with applications to climate tech.

Mar 22, 2021

Solar installers say new rates are slowing demand for rooftop solar | Michigan Radio — Typical solar installation. Source: https://www.michiganradio.org/post/solar-installers-say-new-rates-are-slowing-demand-rooftop-solar

One Big Thought

Physicists are trained to look for invariants. These are variables that stay the same under some transformation. The speed of light, for example, is an invariant across all inertial frames of reference. From that observation alone, the theory of special relativity magically falls out of the math. As such, physicists know that if you find an unchanging variable, you have likely uncovered a deep truth about the universe.

Invariants are less rigorously defined in business or investing, but they still possess significance and inform the creation of useful principles. One of my favorite examples is the “Rule of 40” that illustrates the fundamental tradeoff between growth and profitability. The Rule of 40 variable (call it R) is equal to the sum of the annual revenue (or ARR) growth rate % and the company’s EBITDA (or FCF) % of revenue. You can change one of the latter two variables, and in theory, the other should increase or decrease to offset — yielding a constant R, ideally above 40%:

Illustrative “Rule of 40” graph of revenue growth vs. FCF margin. Source: https://kellblog.com/2017/07/25/the-saas-rule-of-40/

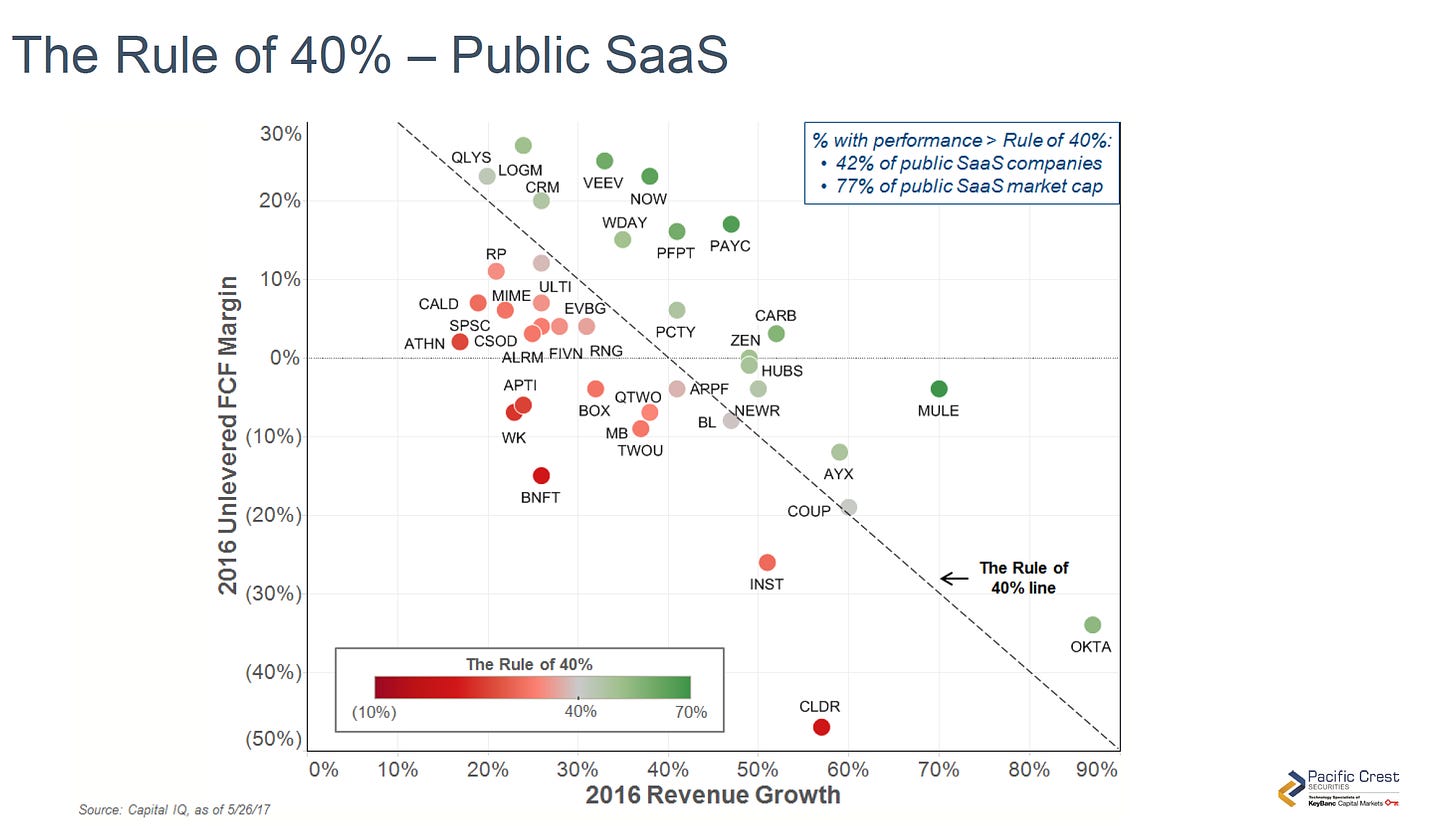
A company with R>40% is a more efficient grower than roughly half of the public comp set. In the above graph, while only 42% of public companies in 2016 had R>40%, that 42% represented 77% of public company value for SaaS companies. R is therefore a highly useful metric to separate great performers from also-ran’s.

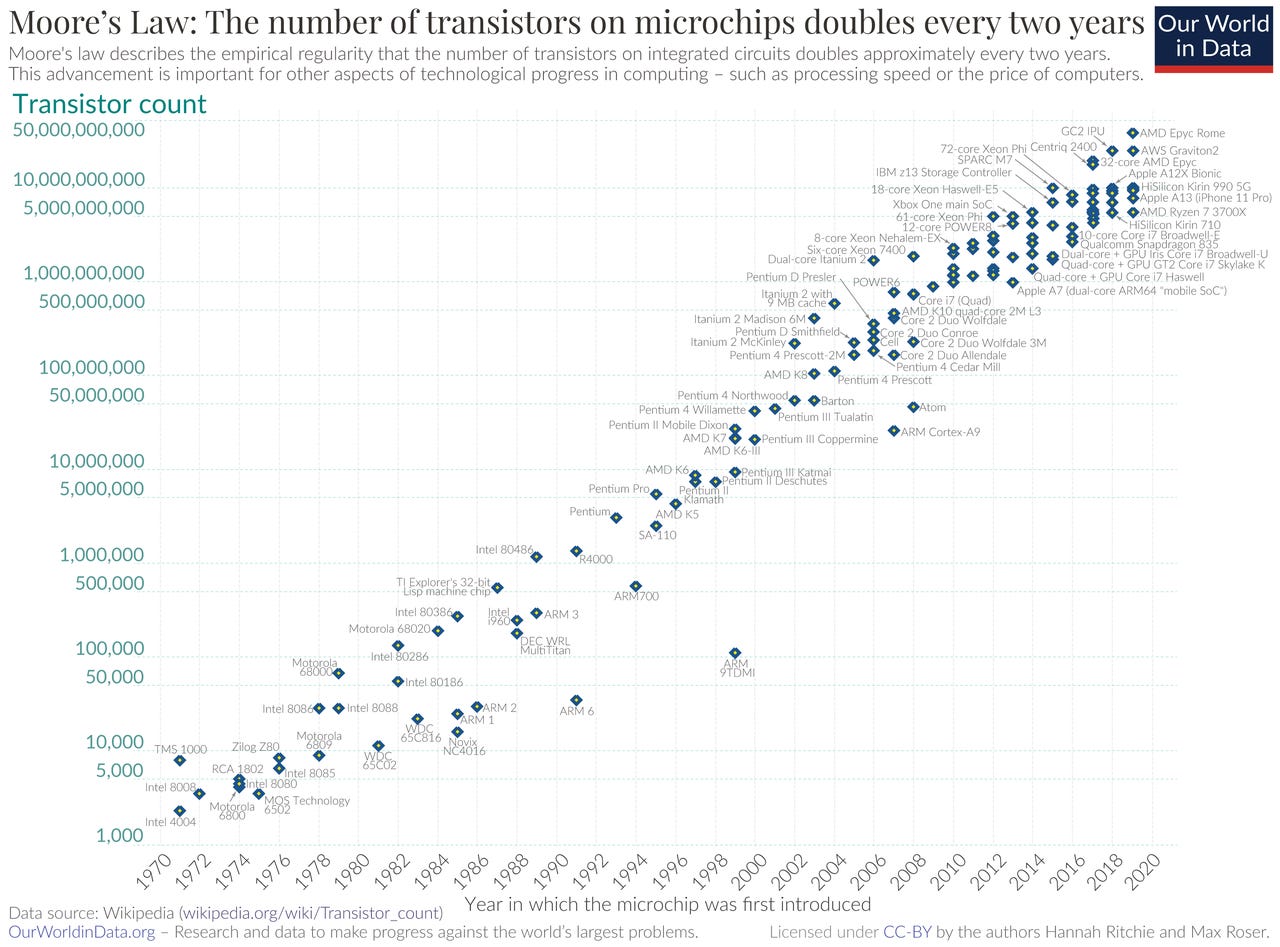
Other invariants can be industry specific. The slope of Moore’s law, which predicts the doubling of the number of transistors on microchips every two years, has been an unrelenting invariant over five decades of progress in semiconductors:

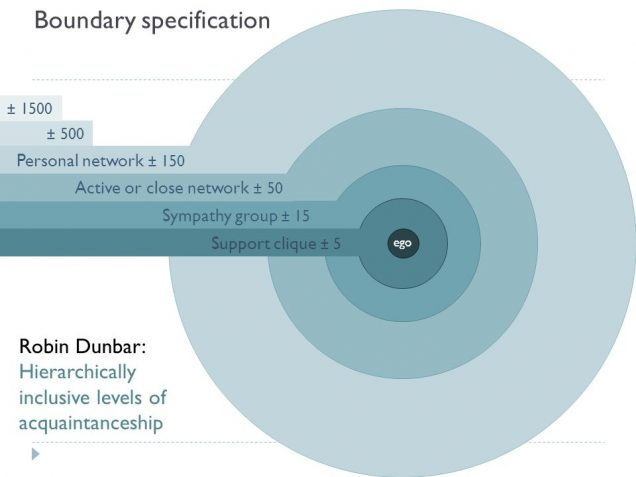
refer to caption — 50 years of Moore’s Law. Source: https://en.wikipedia.org/wiki/Moore%27s_law

Dunbar’s number — the cognitive limit to the number of people with whom humans can maintain substantive, stable relationships — is another invariant in social networking. Social products are routinely built around the Dunbar limit and its related quantities:

Various social invariants. Source: https://sites.bu.edu/cmcs/2018/10/01/the-implications-of-dunbars-number-network-size-and-social-ties/

I’ve been searching for invariants in the arena of climate tech for the last few months. Climate is uniquely tied to the physical world, and therefore its invariants have some relationship to physics. For example, Carnot’s theorem states that a heat engine (a device which does work by harvesting energy moving from a hot to a cold reservoir) cannot operate more efficiently than the maximum provided by this formula:

Carnot Efficiency Formula — Carnot’s theorem. Edit: The original email of this post had T_C and T_H flipped. Whoops!

T_C and T_H are the absolute temperatures of the heat engine’s cold and hot reservoirs, respectively. The most straightforward way to make a heat engine like a power plant produce a higher output is to increase its efficiency by increasing T_H, the combustion temperature. (You could also lower T_C, but if the cool reservoir is the ambient environment that’s less practical.) A fuel like natural gas burns at a fixed temperature at a certain pressure and air concentration (e.g. 1,950 degrees C in standard atmosphere), but you can increase pressure or oxygen concentration to make it burn hotter. Both paths require bigger pressure vessels and more safety precautions and, as such, have diminishing economic returns to scale. Yet, due to Carnot’s theorem, there is some invariant proportionality between the size of a thermal engine (below in MW output) and its efficiency:

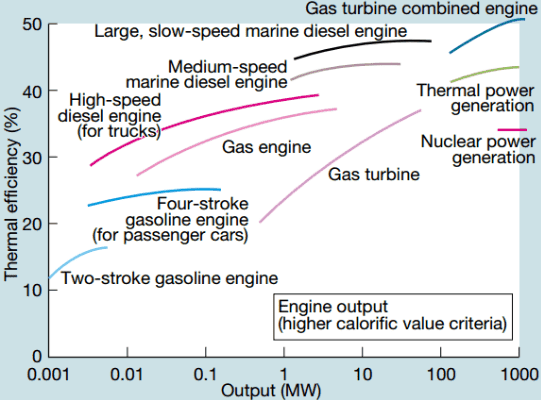
Relationship between size and efficiency of thermal engines. Source: https://www.thermal-engineering.org/what-is-thermal-efficiency-of-steam-turbine-definition/

I credit my former Highland Capital partner Paul Maeder (who is a brilliant investor and mechanical engineer) for pointing out to me that this invariant implies that the business model of thermal power generation is centralized. Carnot’s theorem means bigger power plants are more efficient; therefore, you build them as big as possible (until you see diminishing returns), and transmit their electrons over wires long distances to where they are used. This single invariant relationship explains the architecture of our centralized power grid completely.

Solar photovoltaics (aka solar cells), however, adhere to a different set of physical laws. Solar cells are not heat engines. They convert photons into electrons directly. The maximum efficiency of a solar cell depends more critically on its structural properties (especially a quantum mechanical property called its “bandgap”) than the size of the solar array. Specifically, the so-called Shockley-Queisser limit is the maximum efficiency of a single junction cell in typical solar illumination and varies with the bandgap as shown below:

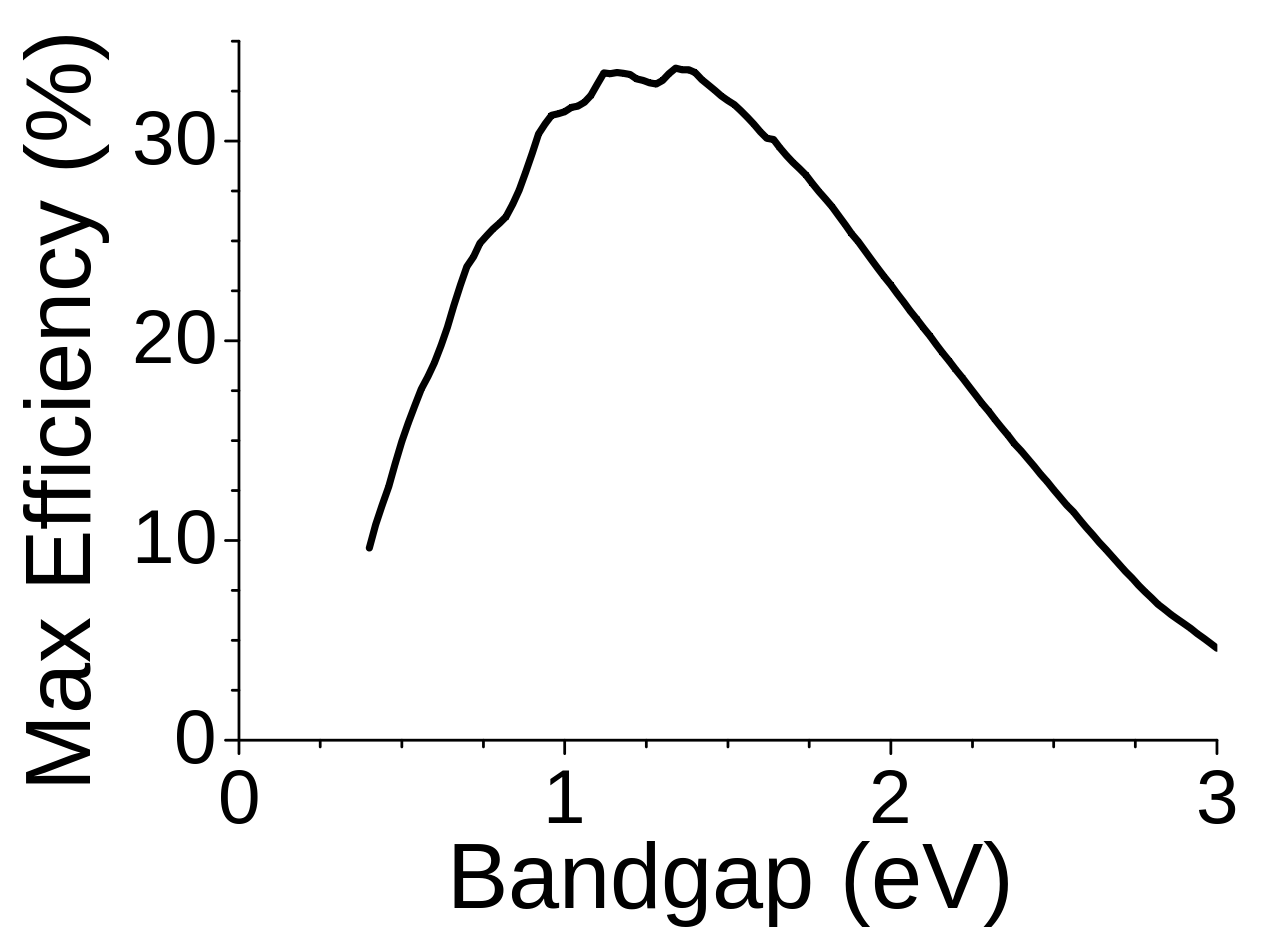
The maximum efficiency of a solar cell is determined not by its size, but by the bandgap of its material. Silicon is 1.1 eV and is close to the maximal point, which is one reason why we use it so frequently in solar cells. Source: https://en.wikipedia.org/wiki/Shockley%E2%80%93Queisser_limit

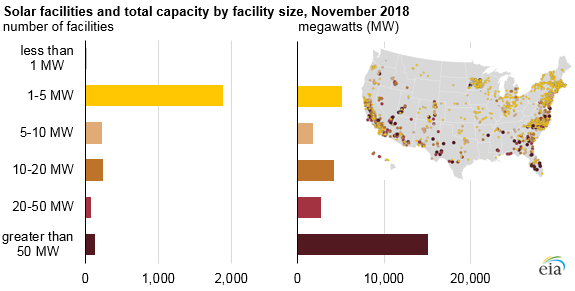
The business model implication is that solar arrays can be as small as an application warrants, without suffering losses in efficiency. Solar is therefore a disruptive source of power because it can be distributed. Efficiency is invariant with size. The two variables are decoupled. This is why nearly 2,000 of the 2,500 non-residential solar facilities in America in 2018 were only 1-5 MW:

solar facilities and total capacity by facility size — Non-residential solar facilities and capacity (MW). Source: https://www.eia.gov/todayinenergy/detail.php?id=38272

Solar constituted 43% of new grid capacity in 2020 and shows no signs of slowing down, thanks to precipitous drops in cost per watt to below $1 on a module level. As shown below, solar costs have followed their own version of Moore’s law, with the exception of a mid-2000’s supply shortage:

Solar is, therefore, disruptive to incumbent thermal power sources due to its independence from Carnot’s theorem and its exponential economies of scale. If you were to build a grid from scratch in the next 5-10 years, you’d be more likely to do so in a distributed manner — with solar and batteries working together. If you had noticed these invariants and invested in enabling tech for distributed solar like micro-inverters (SEDG*, $15B market cap, up 5x in 3 years) or enabling business models like solar financing (RUN*, $11B market cap, up 7x in 3 years), you’d have done quite well.

As such, I believe that the business of energy, the environment, and climate change are inherently tied to physical invariants. We will see more examples in the coming years as the current climate tech boom pushes forward.

If you have more ideas for new invariants for climate tech, please send them along!